다익스트라 알고리즘
- 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘
- 음의 가중치X
- 시간 복잡도 O((V+E)logV) V=정점 개수, E=한 정점의 주변노드
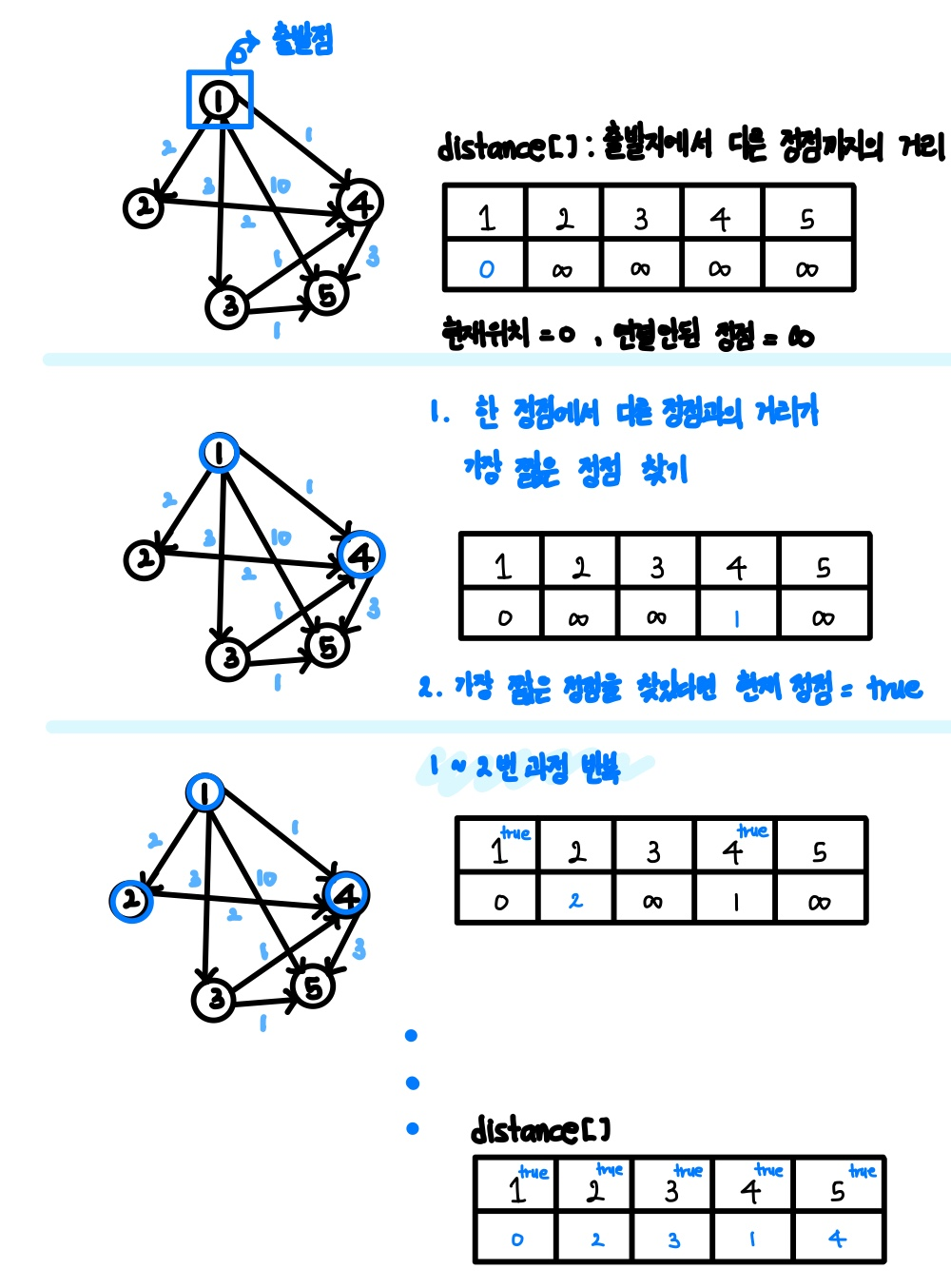
예시
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main{
public static class Node{
int v,w;
public Node(int v, int w) {
this.v = v;
this.w = w;
}
}
static List<Node> list[];
static int [] distance;
static boolean []visited;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
int M = Integer.parseInt(br.readLine());
list =new ArrayList[N+1];
distance = new int [N+1];
visited = new boolean[N+1];
for(int i=1;i<N+1;i++) list[i]= new ArrayList<>();
for(int i=0;i<M;i++) {
st = new StringTokenizer(br.readLine()," ");
int start = Integer.parseInt(st.nextToken());
int arrive = Integer.parseInt(st.nextToken());
int price = Integer.parseInt(st.nextToken());
list[start].add(new Node(arrive,price));
}
st = new StringTokenizer(br.readLine()," ");
int go = Integer.parseInt(st.nextToken()); //시작점
int end = Integer.parseInt(st.nextToken()); //도착점
Arrays.fill(distance, Integer.MAX_VALUE);
distance[go] = 0; //시작점 0으로
int min, current = 0;
for(int i=0; i<N;i++) {
min = Integer.MAX_VALUE;
current = -1;
for(int j=1;j<N+1;j++) { //거리가 가장짧은 정점찾기
if(!visited[j] && distance[j]<min) {
min = distance[j];
current =j;
}
}
if(current == end) break;
for(Node next : list[current]) { //찾은 정점과 연결된 정점들의 거리 저장
if(!visited[next.v] && distance[next.v]> distance[current]+next.w) {
distance[next.v] = distance[current] + next.w;
}
}
visited[current] = true;
}
System.out.println(distance[end]);
}
}
|
cs |
'정리 > 자료구조+알고리즘' 카테고리의 다른 글
| 투 포인터(Two Pointer) (0) | 2021.08.26 |
|---|---|
| 이진 탐색 (Binary Search) 알고리즘 (0) | 2021.07.05 |
| 세그먼트 트리(Segment Tree) (0) | 2021.07.01 |
| 위상정렬 (0) | 2021.06.18 |
| 비트마스크 (BitMask) (0) | 2021.04.21 |